Rubik Unbound: Technical stuff

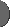I've realized it would take far too long to explain every aspect of the cube, so I'm only describing the user interface here, and it's a very brief description at that. Check the source code rubik.java for details.

So... how the heck does the applet determine where on the cube and what direction any given click-and-drag action corresponds to? Well, the trick is to know in advance what to look for. That makes things a whole lot simpler.

Each time the cube gets drawn on the screen -- i.e. we go from a 3D representation to a 2D projection -- the applet makes notes of where on the screen each vertex ends up, and computes the screen co-ordinates of corresponding "twist areas" (which are basically all the legal places the user could click and drag, that should produce a twist) plus a direction.

This picture, for clarity, shows only one twist area (and its corresponding rotational and drag directions), but each visible side has four of them, making a total of 12. When the user clicks and drags, the applet simply has to test for each of the twist areas, "Was the click point inside it?" and "Is the drag direction close enough to the one that goes with the area?" Both are very simple algebraic operations. If one area tests positive, the applet concludes that a twist has begun and puts the cube into another state.

If not, the dragging is interpreted as a plain rotation and processed accordingly. Though the cube itself isn't rotated. It's easier to just move the "camera", or viewpoint, in the opposite direction. The visible result is the same, at a lower computational cost.

At the beginning of a twist, the cube gets split up into two portions, each with its own share of the physical co-ordinates and the colored pieces. Both of them, however stay in exactly the same physical locations as before, just like during a rotation. What causes the twisted look is that the applet is now using two cameras. A secondary camera is rotated around the twist axis from the primary camera position. Each cube portion is then drawn with respect to its corresponding camera. (The portion whose square side is facing away from the camera(s) is drawn first, and then gets overlapped by the other one in a natural manner.)

While in the split state, at most two twist areas are active at any given moment. Clicking inside them and dragging will progress the current twist clockwise or counter-clockwise. As before, only the angle between the primary and secondary cameras is changed.

Any other dragging moves the primary camera, to give a rotational effect. Since the position of the secondary camera is specified as merely a rotation around a given axis from the primary position, that one will tag along as well, completing the illusion of a rotating cube.

If the camera difference angle is close enough to a multiple of 90 degrees when the user lets go of the mouse button, the applet rounds off the angle and twists the colors of the smaller cube portion accordingly. It then returns the cube to the normal state.